06. Softmax classification - Multinomial classification

이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.

 

이번 포스트는 여러 개의 클래스가 있을 때 그것을 분류하는 Multinomial classification, 그중에서도 가장 많이 사용되는 Softmax classification에 대해 알아보겠습니다.

 

 먼저 Multinomial classification에 대해 알아보겠습니다. 우리는 지난번 포스트에서 Logistic regression에 대해 배웠습니다. Logistic regression을 부르는 다른 이름은 binary classification으로, 데이터를 1과 0 두 그룹으로 나눌 때 사용되는 모델입니다. 반면 Multinomial classification은 데이터를 셋 이상의 그룹으로 나누기 위해 binary classification을 확장한 모델입니다. 따라서 우리는 Logistic classification을 근본으로 Multinomial classification을 이해하면 보다 쉽게 이해할 수 있을 것입니다. 아래는 Logistic regression를 표현하는 그래프와 도식의 한 예시입니다.

그래프 1.1. Logistic regression의 hypothesis

도식 1.1 Logistic regresison의 과정

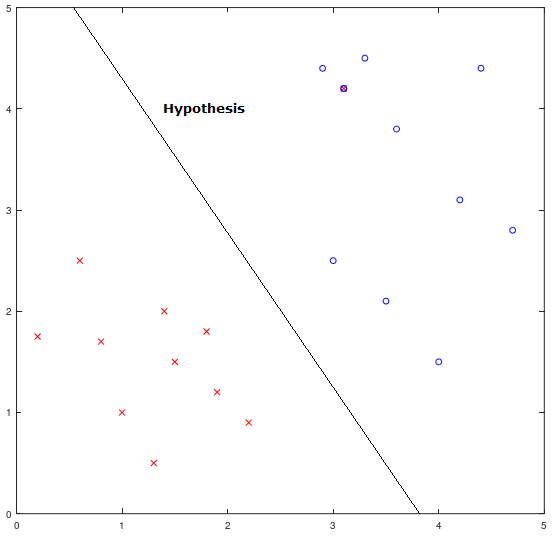
그래프 1.1은 데이터를 x와 o 두 그룹으로 구분되어 있습니다. 이 떄 두 데이터 그룹 사이의 Hypothesis는 데이터를 구분 지어주는 적절한 직선으로 보입니다. 이제 아래 도식 1.1을 살펴보겠습니다. 도식은 H(x)를 z라 놓은 채 sigmoid 함수에 넣어(g(z)) 예측값을 1과 0으로 구분하는 과정을 나타냅니다. sigmoid 함수의 그래프와 예측값을 얻는 과정에 대한 자세한 내용은 05. Logistic Regression(1)을 확인해주시길 바랍니다. 참고로 앞으로 많이 보게 될 도식의 Y(앞으로는 Ŷ으로 표현하겠습니다)는 Y-hat이라고 부르며 예측값(predicted value)를 말합니다. 이로써 Logistic Regeression에 대해 간략히 복습해보았습니다.

 

 그렇다면 이제 Multinomial classification을 알아보겠습니다. 먼저 Training Data set의 x와 y를 준비합니다. x1과 x2는 각각 공부한 시간, 수업에 참석한 횟수, y는 성적 등급(A-C)을 말합니다.

x1 (hours)	x2 (attendance)	y (grade)
10	5	A
9	5	A
3	2	B
2	4	B
10	1	C

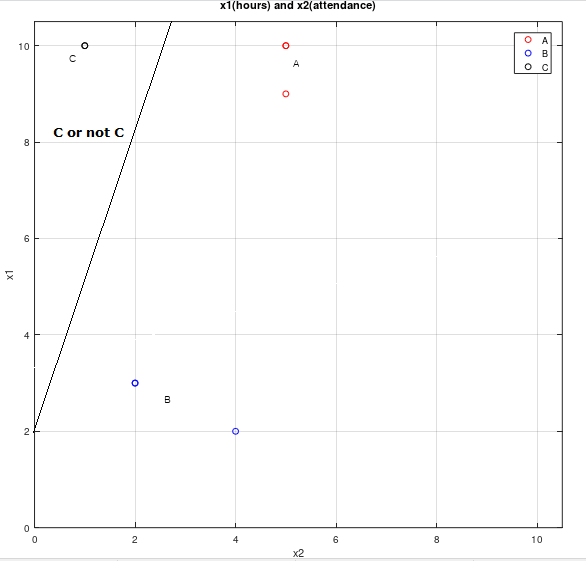
표의 데이터를 그래프로 그려 자세히 알아보겠습니다.

그래프 2.1.  x1 and x2, octave에서 작성되었습니다.

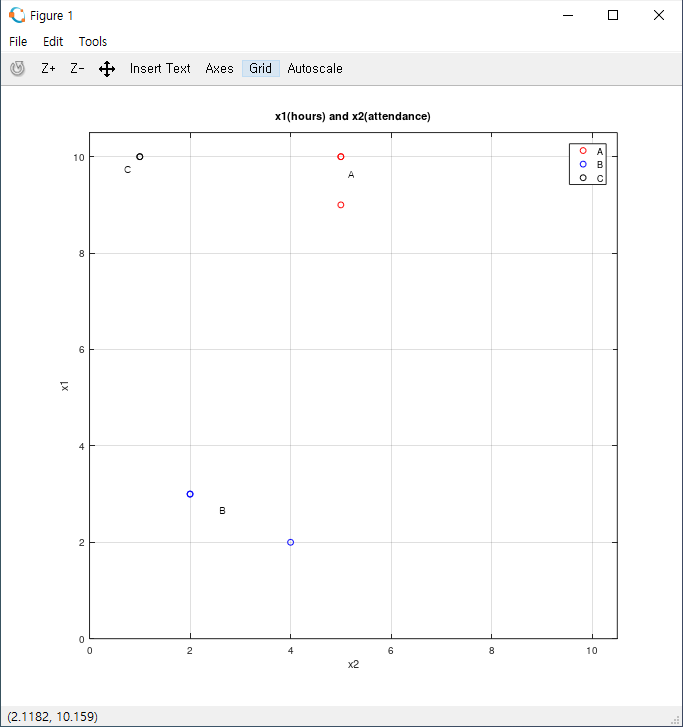
그래프를 보면 grade(y)에 따라 데이터들이 군집을 이룬 모양을 볼 수 있습니다. 만약 우리가 이 데이터들을  A or not A와 같은 방법으로 분류한다면, Binary classification만으로도 Multinomial classification을 구현할 수 있습니다. 시각적으로 이해하기 위해 (A or not A), (B or not B), (C or not C)의 세 개의 각각 다른 Binary classification을 표현한 그래프의 한 예시들을 보겠습니다.

그래프 2.2. case: A or not A

그래프 2.3. case: B or not B

그래프 2.4. case: C or not C

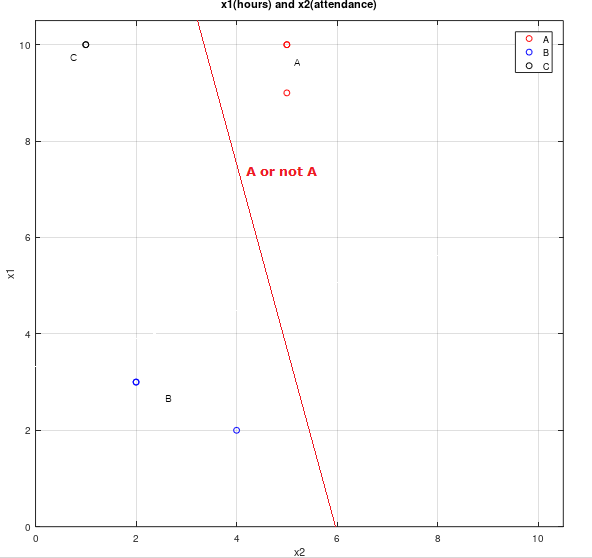
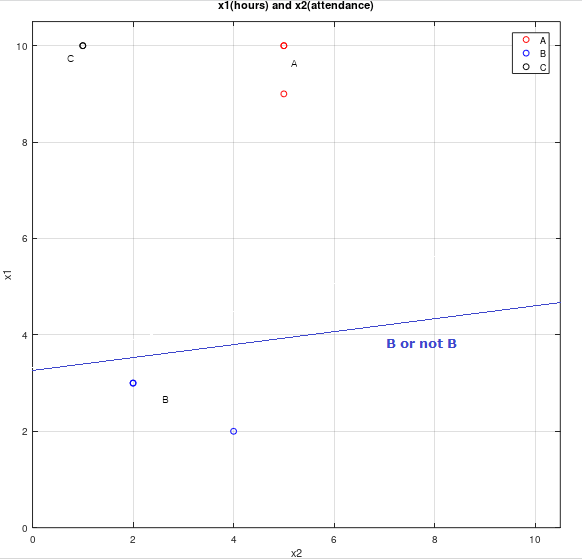
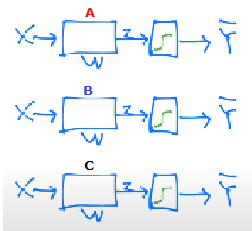
우리는 Logistic regression에서 예측값을 구하는 과정을 표현하는 도식 1.1에 위의 독립된 세 경우(A or not A, ...)를 대입하면 아래의 도식으로 나타낼 수 있습니다.

도식 2.1. 원본 출처: 모두를 위한 딥러닝 

위 도식을 실제로 구현하기 위해서는 먼저 우리는 행렬을 이용하여 표현해야합니다. 아래 행렬은 각각의 H(X) = WX를 표현한 경우(수식 1.1)와 세 경우를 하나의 W행렬(3 x 3 행렬)로 합쳐 H(X)를 표현한 경우(수식 1.2)를 보여줍니다. 참고로 H(X) = XW로 표현하는 것이 일반적으로 지향되지만 이번에는 가독성을 위해 W를 행 벡터로, X를 열 벡터로 두어 H(X) = WX로 표현하였습니다. 

수식 1.1. 각각의 독립된 H(X) = WX

 

수식 1.2. 세 가지 W행렬을 하나로 합쳐 표현한 H(X) = WX

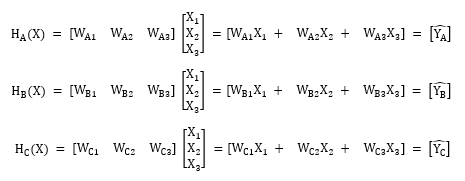
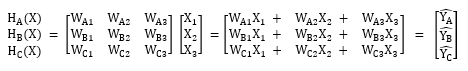
주목할 점은 수식 1.2입니다. 도식2.1을 그대로 옮긴 수식 1.1에서는 각각의 경우에 대해 H(X)를 따로 표현하여 세 개의 독립된 classification을 구현하였지만, 수식 1.2에서는 W를 하나의 벡터로 묶어 처리합니다. 이렇게 수식 1.2와 같이 표현하는 방법이 바로 Multinomial classification입니다. 실제로 수식 1.2의 Multinomial classification은 수식 1.1의 Logistic regresison 방식을 토대로 여러 클래스가 있는 경우에 각각을 묶어 하나의 벡터로 표현하는데, 이로써 한 번에 계산이 가능하고 세 개의 독립된 classification처럼 동작을 합니다.

 다만, 한 가지 궁금한 점이 있습니다. 도식 2.1에서는 sigmoid 모듈을 통해 데이터를 처리합니다. 물론 수식 1.2에서 각각의 Ŷ에 sigmoid 모듈을 적용하여 데이터를 처리하면 되지만, 이런 방식은 Logistic regression에 비해 큰 이점이 없어보입니다. 따라서 다음 포스트에서는 sigmoid 모듈을 굉장히 효율적이고 간단하게 하는 방법인 Softmax에 대해 자세히 알아보겠습니다.