2020. 4. 13. 01:45ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.
이번 포스트는 저번 포스트에 이어 Logistic regression(로지스틱 회귀)의 cost function(비용 함수)과 optimizer - Gradient descent(경사 하강법)에 대해 알아보겠습니다.
Logistic regression의 cost function에 대해 알아보겠습니다. 먼저 아래 그림을 보겠습니다.

로지스틱 회귀에서는 데이터를 분류해주는 적절한 Hypothesis가 필요합니다. 왼쪽의 두 직선은 데이터를 잘 분류하지는 못하는 것으로 보이는 반면 오른쪽의 직선은 데이터 ■과 ▲을 분류해주는 적절한 직선입니다. 따라서 Hypothesis가 오른쪽 직선일 때 cost가 0이므로 우리는 로지스틱 회귀에서 오른쪽 직선과 왼쪽 직선의 차이로 cost function을 표현할 수 있습니다.
이제 Logistic Regressioin의 cost function에 대해 알아보겠습니다. 먼저 Simple Linear regression에서 배운 cost function은 다음과 같습니다.

이제 Simple Linear regression의 cost function에 Logistic regression의 Hypothesis(g(z) = 1 / (1 + e^(-z)), z = tf.matmul(X, W) + b)를 대입한 그래프를 그려보면 아래와 같습니다.

아래 그림은 g(z)에서 Y를 뺀 결과 오른쪽의 굴곡진 그래프 모양이 나온다는 것을 보여줍니다. 따라서 위 그림처럼 cost 그래프는 이미 굴곡진 그래프를 제곱하니 실제로 굉장히 많은 굴곡점을 가집니다. 그렇다면 이런 그래프의 모양이 어떤 경우에 문제가 될까요? Gradient descent를 이용하여 minimize cost를 찾으려 할 때 어떤 점에서 시작하느냐에 따라 지역적 최솟값(Local minimum)을 전역적 최솟값(Global minimum)으로 착각하여 실제와 다른 결괏값을 얻을 수도 있습니다. 이는 cost function이 not convex function의 모양을 가지기 때문인데, convex function에 대한 상세한 설명은 03. How to minimize cost - Gradient descent에서 확인하실 수 있습니다.
그렇다면 우리는 Logistic regression의 cost function을 재정의할 필요가 있습니다. 결론부터 말하자면, Logistic regression에서의 cost function은 다음과 같습니다.

위 식을 보면 y값에 따라 c(H(x), y)가 다르게 정의됩니다. 먼저 y = 1 일 때의 c(H(x), y) 그래프를 보겠습니다.
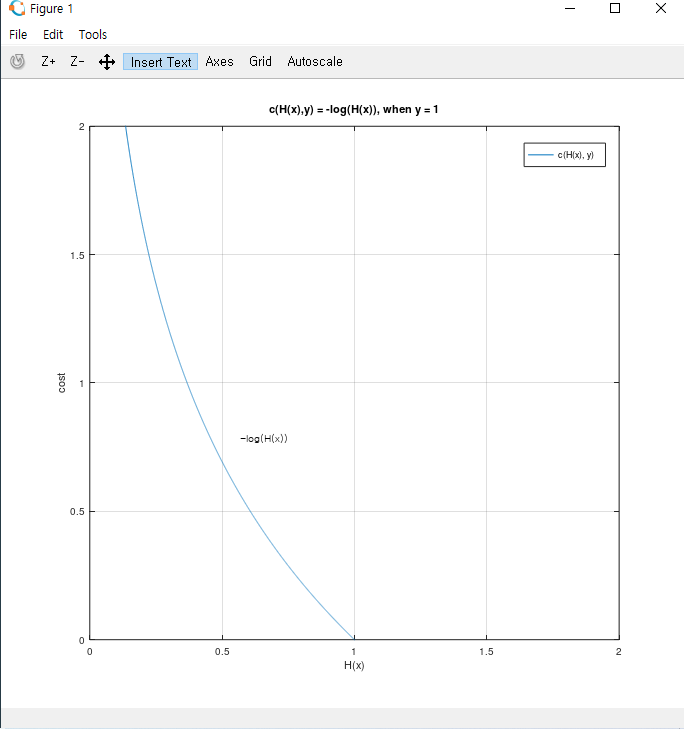
y = 1일 때 c(H(x), y)는 -log(H(x))입니다. 이미 알고 있듯이 cost는 예측값과 실제값의 오차와 비례합니다(예측값과 실제값이 비슷해질수록 cost가 줄어들어 0에 가까워지지만, 예측값과 실제값이 멀어지면 cost가 커집니다). 실제로 위 그래프 2.1에서 H(x) = 1일 때 cost = 0이지만, H(x) -> 0 일 때 cost는 무한대(∞)로 발산합니다. 따라서 -log(H(x))는 y = 1일 때의 cost function으로 적절해 보입니다. 그렇다면 왜 log를 사용하여 cost function을 정의할까요? 이유는 간단합니다. 로지스틱 회귀의 Hypothesis 1 / (1 + e^(-z))에 있는 자연상수 e와 상극인 log를 사용하여 굴곡을 없애고 convex 한 모양의 그래프를 만들 수 있기 때문입니다. 그렇다면 y = 0일 때의 c(H(x), y)를 살펴보겠습니다. 그래프는 아래와 같습니다.

y = 0일 때 c(H(x), y)는 -log(1 - H(x))입니다. y = 1일 때와 반대로 H(x)가 0일 때 cost는 0에 수렴하며 1에 가까워질수록 무한대로 발산하므로 cost function으로 적절해 보입니다. 따라서 로지스틱 회귀의 cost function을 정리하면 아래의 식으로 표현할 수 있습니다.

아래의 C(H(x), y) = -ylog(H(x))... 는 위의 수식을 한 줄로 표현한 수식으로, 마찬가지로 y의 값에 따라 C(H(x), y)가 정의됩니다. 이렇게 cost function을 한 줄로 표현함으로써 바로 뒤에서 배우는 Gradient descent를 편리하게 사용할 수 있고 텐서플로우 코드를 보다 보기 좋게 작성할 수 있습니다. 실제로 텐서플로우에서 cost function을 구현하는 코드에 대해서는 다음 포스트에서 알아보겠습니다.
이번에는 optimizer - Gradient Descent에 대해 알아보겠습니다. 먼저 optimizer는 수학적으로 많이 사용되는 단어입니다. 수리 계획 도는 수리 계획 문제라고도 하고 딥러닝에서는 학습 속도를 빠르고 안정적이게 하는 것이라고 말할 수 있습니다. 그렇다면 Logistic regression에서 Gradient descent(경사 하강법)는 optimizer 방법 중 하나라고 말할 수 있습니다. 우리는 이미 03. How to minimize cost - Gradient descent에서 Gradient descent에 대해 배운 적이 있습니다. 로지스틱 회귀에서의 경사 하강법 또한 다르지 않습니다. 단, 수식 3.1을 보면 cost function이 y = 1과 y = 0의 경우로 나뉘어 정의되었기 때문에, 편의상 아래의 한 줄로 정의된 수식을 사용하여 Gradient descent algorithm에 대입한다는 특징이 있습니다. 그렇다면 아래의 식을 통해 Logistic regression - Gradient descent를 보겠습니다.

이번 포스트에서 우리는 Logistic regression(로지스틱 회귀)의 cost function(비용 함수)과 optimizer - Gradient descent(경사 하강법)에 대해 알아보았습니다. 다음 포스트는 05. Logistic Regression(1)과 05.1 Logistic Regression(2)에서 배운 내용을 실제로 텐서플로우 코드로 구현해보겠습니다.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 06. Softmax classification - Multinomial classification (0) | 2020.04.18 |
|---|---|
| 05-2. Logistic Regression(3) - Logistic Regression LAB (0) | 2020.04.17 |
| 05. Logistic Regression(1) (0) | 2020.04.10 |
| 04-1. Multi-variable Linear Regression LAB (2) | 2020.04.07 |
| 04. Multi-variable Linear Regression (0) | 2020.04.05 |