06-1. Softmax classification

이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.

 

이번 포스트는 저번 포스트에 이어 Softmax classification와 Cost function을 설계하는 과정에 대해 알아보겠습니다. 먼저 저번 포스트의 내용을 간략히 복습해보겠습니다. Multinomial classification(수식 1.1)은 W를 하나의 행렬(3 x 3)로 묶어 곱해 결괏값이 하나의 벡터(3 x 1 Ŷ벡터)로 나와 데이터를 처리하는 것이 편리하다는 장점이 있습니다. 다만 우리는 Sigmoid를 적용하는 적절한 방법을 이용해 Ŷ(A B C)를 일괄적으로 표현할 필요를 느꼈습니다.

수식 1.1. Multinomial classification

 따라서 이번 포스트에서 우리는 수식 1.1의 Ŷ에 sigmoid 모듈을 효율적이고 간단하게 적용하는 방법인 Softmax를 배우고, 나아가 Softmax classification의 Cost function을 해석해보겠습니다. (설명에 나오는 손그림들은 강의와 udacity를 인용하여 iPad에서 다시 그렸습니다.)

 

그림 1. Softmax function

위의 그림 1에서 H(X) = WX를 계산해 Ŷ(A, B, C)에 상응하는 벡터로 (2.0, 1.0, 0.1)을 구했다고 가정해보겠습니다. 하지만 우리는 이 값들을 1. 0 <= P <= 1, 2. ∑P = 1, 이 두 조건을 만족하는 확률의 형태로 표현하는 것을 원합니다. 이처럼 값을(score) 확률로(to probability) 바꿔주는 것이 바로 Softmax function입니다. 그림 1에서  Softmax function hypothesis을 볼 수 있습니다.

그림 2. One-hot encoding, change probabilities to static value 1 or 0

이후 Softmax()를 통해 얻은 벡터 P를 One-hot encoding을 사용하여 1과 0으로 나타냅니다. 위 그림의 과정을 순차별로 살펴보겠습니다. 먼저 그림의 벡터 P는 Ŷ(A = 2.0, B = 1.0, C = 0.1)를 softmax()에 넣어 얻은 벡터로, (0.7, 0.2, 0.1)의 확률 값을 가집니다. 이 벡터 P를 One-hot encoding(표현하고 싶은 값에 1을 부여하고, 다른 값에는 0을 부여하는 벡터 표현 방식입니다)을 사용해 가장 큰 값(0.7)에 1을, 나머지 값(0.2, 0.1)에 0을 정합니다. 최종적으로 우리는 One-hot encoding 된 값을 참조하여 하나('A')를 선택할 수 있습니다. 다음은 Softmax의 Cost function인 Cross-entropy에 대해 알아보겠습니다.

그림 3. Cost function (Cross-entropy)

위 그림은 Softmax의 Cost function인 Cross-entropy에 대해 설명하고 있습니다. softmax를 통해 구한 예측값(왼쪽) S(Ŷ)을 S, One-hot encoding 된 실제값(오른쪽)을 L로 놓은 채 cost function을 구하면 위 그림의 식(Cross-entropy)을 얻을 수 있습니다. 그렇다면 cost function이 왜 이런 식으로 도출되는지 알아보겠습니다. 먼저 Cross-entropy 식을 다시 보겠습니다.

수식 2.1. Cross-entropy

그림 4. Cross-entropy process

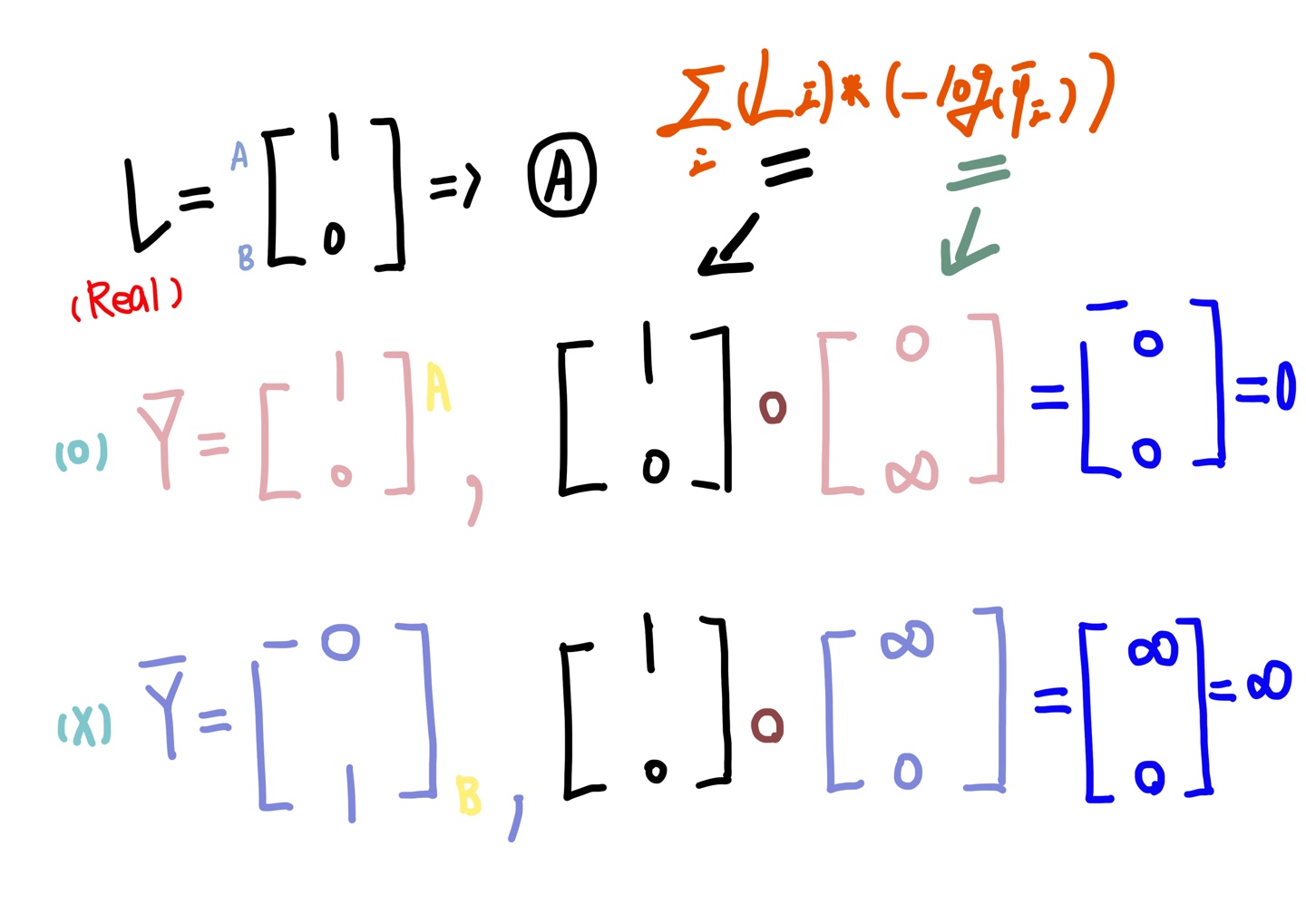
수식 2.1의 오른쪽 식에 주목해보겠습니다. 오른쪽 식은 (-)를 ∑log에 넣어 L과 (-log(Ŷ))의 곱으로 표현했습니다. 참고로 이때의 곱은 흔히들 알고 있는 일반적인 행렬곱이 아니라 아다마르 곱(Hadamard product)으로, 같은 크기의 두 행렬의 각 성분을 곱하는 연산입니다. element product로도 불리는 아다마르 곱(곱셈 기호: ○)은 m x n 꼴의 두 행렬의 각 성분을 곱한다는 점에서 일반 행렬곱과 차이가 있습니다. 수식 2.1의 오른쪽 식이 이해가 되었다면 그림 4를 보겠습니다. 실제값을 갖는 벡터 L에서 A(위), B(아래)에 해당하는 값이 1, 0로, 벡터 L은 A를 예측합니다. 이제 벡터 L과 아래의 예측값을 갖는 두 개의 벡터 Ŷ을 Cross-entropy에 넣어 계산해보겠습니다. 아래 그림 5는 두 개의 벡터 Ŷ 와 벡터 L을 계산하는 과정을 나타낸 그림입니다.

그림 5. Cross-entropy calculation

 먼저, 벡터 L과 벡터 Ŷ(위)를 계산하는 과정을 보겠습니다. -log(Ŷ)는 1일 때 0에 수렴하고, 0에 가까워질수록 무한대(∞)로 발산하는 모양을 보입니다(아래 그래프 1.1 참조). 따라서 -log에 Ŷ벡터 [1 0]을 넣으면 [0 ∞]으로 계산되고, 이 요소와 L벡터의 요소를 아다마르 곱하면 영 벡터가 나옵니다. 이 벡터를 총합(∑)한 값이 바로 Softmax classification의 cost입니다. cost가 0인 것으로 보아 벡터 Ŷ(위)는 예측값이 실제값과 동일하다고 볼 수 있겠습니다. 매우 좋은 예측이라고 할 수 있습니다.

 반대로 위와 같은 순서로 벡터 L과 벡터 Ŷ(아래)를 계산하면 cost가 무한대(∞)로 발산하는 굉장히 큰 값을 갖습니다. 따라서 이러한 경우는 벡터 Ŷ(아래)가 예측값이 실제값과 동떨어진, 잘못된 예측을 하고 있다고 볼 수 있겠습니다. 벡터 Ŷ(위)와는 다르게 매우 나쁜 예측이라고 할 수 있습니다.

그래프 1.1. -log(S) 그래프

이로써 우리는 softmax clssification의 cost function인 Cross-entropy에 대해 알게 되었습니다. 그렇다면 이전에 배운 Logistic cost와 Cross-entropy를 비교해보겠습니다.

수식 3.1. Logistic cost(위)와 Cross-entropy(아래)

결과부터 말하자면, 사실 위의 두 cost function은 표현만 다를 뿐 같은 식입니다. 이를 증명하기 위해 Logistic cost에서 y를 p1, H(x)를 q1, y-1을 p2, 1-H(x)를 q2로 치환하면 -(p1·log(q1) + p2·log(q2))로 표현할 수 있습니다. 아래는 치환한 식에 ∑를 써서 변형한 식(좌)과 일반화한 식(우)입니다.

수식 4.1. Logistic cost 변형(좌), 일반화(우)

Logistic cost의 H(x)와 y가 각각 Cross-entropy의 S, L에 대응하기 때문에 Logistic cost를 변형한 수식(좌)을 일반화한 식(우)이 결국 Cross-entropy와 같다는 것을 증명할 수 있습니다. 또 다른 방법으로 실제값(y, L)과 예측값(H(x), S)이 각각 0과 1인 네 가지 경우를 모두 계산해보아도 Logistic cost = Cross-entropy라는 결과가 나옵니다. 이외의 다양한 방법은 강의 아래의 댓글을 참고해주시길 바랍니다.

 

이때까지의 Cross-entropy는 모두 하나의 데이터 셋에 대해 살펴보았습니다. 그렇다면 여러 개의 Training set이 있을 때의 Cost(Loss) function은 어떻게 표현할까요? 아래의 식을 살펴보면 Loss는 모든 Training set(m)에 대한 예측값과 실제값의 오차를 더한 값의(∑D(S, L)) 평균한(1/m) 값을 방법을 사용합니다.

수식 5.1. Cost function Training set>1

 

이번 포스트에서 우리는 Softmax classification의 hypothesis와 cost function인 Cross-entropy의 개념을 배우고 Cross-entropy를 직접 계산해보았습니다. 이번 포스트에서는 굉장히 많은 식들을 볼 수 있는데, 단순히 암기하는 것보다는 그림의 순서에 맞춰 논리적인 과정으로 따라가다 보면 보다 식과 개념을 쉽게 이해할 수 있을 것입니다. 다음 포스트는 이번 포스트에서 배운 Softmax classification을 텐서플로우로 구현해보겠습니다.