2021. 12. 24. 03:05ㆍAI/ML
이 포스트는 허민석 님의 유튜브 머신러닝 내용을 정리한 글입니다. 실습 코드는 도서 나의 첫 머신러닝/딥러닝에서 발췌해왔습니다.
kNN, 최근접 이웃법 알고리즘에 이어 이번 포스트에서는 Decision Tree(결정 트리, 의사결정 트리)와 ID3(Iterative Dichotomiser 3) 알고리즘에 대해 알아보겠습니다.
전 포스트에서 kNN 알고리즘을 설명하며 유유상종이라는 사자성어를 예로 들어 설명했는데, 이번에는 Decision Tree를 쉽게 이해하기 위해 스무고개를 예로 들어보겠습니다. 우리는 스무고개를 할 때 예 / 아니오에 해당하는 질문을 통해 후보군을 좁혀 나갑니다. 아래의 그림처럼 정답이 "보스 베이비"라고 할 때 먼저 첫 번째 질문으로 "사람인가요?"를 했다면, "아니오"라는 답변을 통해 후보군을 사람이 아닌 분류로 좁혀나갈 수 있습니다. 다음 질문으로 "애니메이션에 나오는 캐릭터인가요?"에 대해서는 "예", 그다음 질문으로 "캐릭터가 성인인가요?"에 "아니오"라는 답변을 받았다면, 정답이 될 수 있는 후보를 굉장히 많이 좁힐 수 있습니다. 마지막으로 "캐릭터가 정장을 입고 있나요?"라는 질문을 한다면, "예"라는 대답과 함께 우리는 정답이 보스 베이비임을 맞출 수 있습니다. 이렇듯 스무고개와 동일한 방식으로 어떤 특징(Feature)이나 속성(Attribute)을 통해 나무 구조로 나타내며 데이터를 분류하는 방식이 Decision Tree(결정 트리) 알고리즘입니다.

이제 허민석 님의 유튜브 영상에 나오는 "겨울에 찍은 가족사진 찾기"를 Decision Tree를 통해 찾아보겠습니다. 먼저 우리는
1. 컴퓨터에게 무엇을 해야 하는지를 알려줘야 합니다. 이 과정에는 define problem(겨울에 찍은 가족사진 찾기)과 collect training data(train data로 8개의 사진 모으기)이 포함됩니다. 위의 설명대로 겨울에 찍은 가족사진을 찾는 문제 상황을 정의하고, 훈련 데이터로 사용될 데이터들을 모읍니다. 현재 8장의 훈련 데이터 사진이 있으며, 이 중 겨울에 찍은 가족사진을 찾는 것이 컴퓨터에게 요구됩니다. 왼쪽 위에서부터 1, 2, 3, 4, 왼쪽 아래에서부터 5, 6, 7, 8이라고 하겠습니다.

이제 우리는 2. Decision Tree를 생성합니다. 이때 우리는 먼저 extract data(속성을 정한 다음 사진별 데이터 추출) 다음 build a tree(결정 트리 생성) 작업을 합니다. 데이터의 속성이 데이터 추출 및 분류에 굉장히 중요한 점으로, 이번에는 만화 캐릭터인지(cartoon caracter?), 겨울인지(winter?), 사진에 나오는 인물이 1명 이상인지(more than 1?)의 속성으로 데이터를 추출하겠습니다. 이제 우리는 표로 정리하여 데이터를 한눈에 볼 수 있으며 속성들을 토대로 결정 트리를 생성할 수 있습니다.
| img | cartoon caracter? | winter? | more than 1? |
| 1 | No | Yes | No |
| 2 | Yes | No | Yes |
| 3 | Yes | No | Yes |
| 4 | No | Yes | No |
| 5 | No | No | Yes |
| 6 | No | Yes | Yes |
| 7 | Yes | No | Yes |
| 8 | No | Yes | No |
이제 Decision Tree를 만듭니다. 사실 Decision Tree를 만들 때는 어떤 속성을 먼저 사용하는지에 따라 효율성이 달라지는데, 이 내용은 조금 있다 ID3 알고리즘을 알아볼 때 수학적으로 분석해 볼 것입니다. 지금은 attribute의 순서대로 Decision Tree를 그려보면 아래의 그림과 같습니다.

이제 Decision Tree를 토대로 3. deploy machine(머신이 작동하며 학습하는 작업)과 4. 테스트 데이터들에 대한 테스트를 거치게 됩니다. 여기까지가 Decision Tree 알고리즘 작동 방식에 대한 설명이며, 처음 말했던 것처럼 스무고개를 생각하면 이해가 보다 쉬울 것입니다.
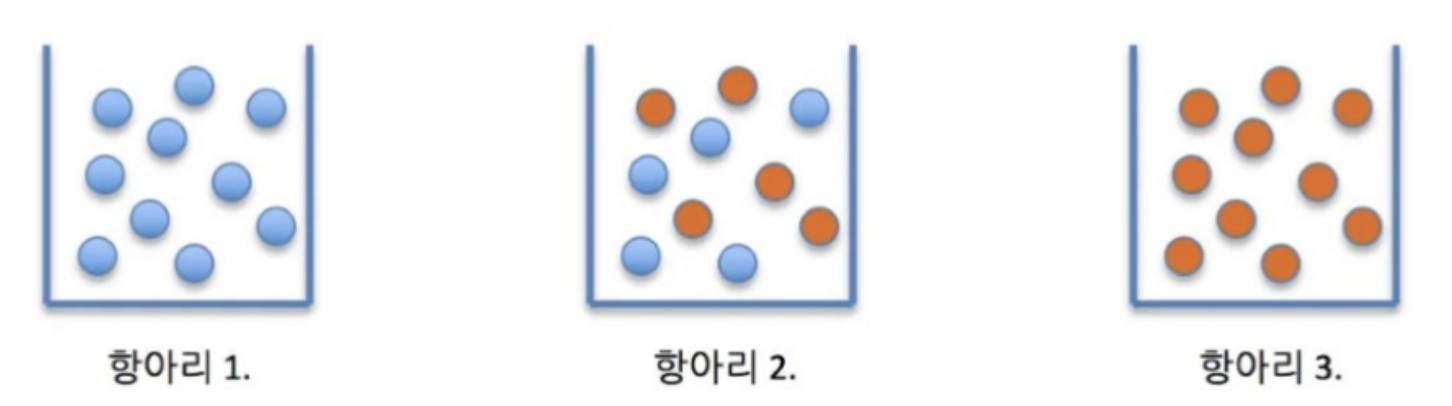
이제 보다 효율적인 Decision Tree를 위해서는 어떻게 해야 할까요? 먼저 불순도(impurity)와 엔트로피(entrophy)에 대해 이해하고 넘어가겠습니다. 우선 불순도는 한 범주 내 다른 범주의 개체들이 얼마나 포함되어 있는지에 대한 지표입니다. 반대되는 개념으로는 순도(purity)가 있으며, 아래의 그림을 보면 항아리 1과 3에는 파란색 공과 빨간색 공들만 들어 있으나, 항아리 2에는 파란색 공들과 빨간색 공들이 섞여 있는 모습을 볼 수 있습니다. 항아리 1과 3은 불순도 0%, 순도 100%이며 항아리 2는 불순도가 높고 순도가 낮은 상태라고 말할 수 있습니다.
불순도를 수치화한 지표에는 엔트로피가 대표적입니다. 엔트로피는 특정 정보에 대한 불확실성을 의미하며, 한 단어로 복잡함을 의미합니다. 방이 어지러운 상태면 방의 엔트로피가 높은 상태이고, 잘 정리 정돈되어 있는 상태면 엔트로피가 낮은 상태라고 말할 수 있습니다. 불순도를 엔트로피로 수치화하여 최적의 Decision Tree를 생성하는 알고리즘이 이제부터 알아볼 ID3 알고리즘이며, ID3는 Iterative Dichotomiser 3의 약자로, 이분하다는 뜻의 프랑스어인 Dichotomiser을 토대로 해석해보면, "반복적으로 이분하는 알고리즘"이라는 의미이며 결국 불순도가 낮은 방향으로, 다시 말해 엔트로피가 낮은 방향으로 Decision Tree를 구성하는 것이 효율적임을 의미합니다. 위의 "겨울에 찍은 가족사진 찾기" 예시를 보며 설명하겠습니다.

처음 8장의 사진에서, 분류에 어떤 속성을 사용하느냐에 따라 분류되는 사진의 수가 달라지는 것을 확인할 수 있습니다. 예를 들어 위의 왼쪽 사진에서처럼 "Cartoon Character?" 속성이 분류 기준으로 사용된다면 Yes / No 분류기를 거쳐 남는 사진은 4개입니다. 반면 중간과 오른쪽 사진에서처럼 "Winter?"과 "More than 1?" 속성이 분류 기준으로 사용된다면 분류기를 거쳐 남는 사진은 5개가 됩니다. 물론 "최종적으로 남는 데이터는 어차피 하나이므로 큰 차이가 없지 않나요?" 하는 의문점이 들 수 있지만, 실제 모델을 만들어 학습 시에는 데이터의 양이 방대하므로 분류기를 거쳐가며 남는 데이터의 개수가 가장 작아지는 속성을 사용하는 것이, 다른 말로 엔트로피가 가장 작아지는 속성을 사용하는 것이 효율적인 알고리즘이라고 할 수 있습니다. 또한 ID3에는 information gain(정보 획득)의 개념을 알아두어야 하는데, information gain은 base entrophy에서 new entrophy을 뺀 것을 의미합니다. 예를 들어 위 사진의 왼쪽에서 분류 이전 사진의 개수(base entrophy)는 8개이며, 속성 "Cartoon Character?"로 분류한 뒤 남은 사진의 개수(new entrophy)는 4개로, 정보 획득은(had 8 pictures - now just 4 left, 8-4) 4입니다. 결과적으로 entrophy는 적은 방향으로, information gain은 큰 방향으로 속성을 선택하는 것이 중요하다고 할 수 있습니다. 이해를 돕기 위해 사진의 개수로 엔트로피를 설명했지만, 실제 엔트로피는 공식에 의해 수치적으로 계산되며, 엔트로피를 통해 information gain을 계산한 다음 최적의 속성을 선택하여 알고리즘을 구성하게 됩니다. 이제부터 처음 상태의 엔트로피와 첫 번째 단계를 거친 다음의 엔트로피 계산을 통해 information gain을 얻은 다음, 어떤 속성이 information gain이 가장 높은지(다른 말로 가장 효율적인 첫 번째 분류 속성을 찾는 과정입니다) 알아보겠습니다.
먼저 처음 상태의 엔트로피(base entrophy)를 계산해보겠습니다. 공식에서 p는 확률을 의미하며 p(+)는 분류기에 통과된, p(-)는 분류기에서 걸러진 사진으로 이해하는 것이 좋습니다. 엔트로피를 구하는 공식은 다음과 같습니다.
Entrophy([+, -]) = -p(+) log(p(+)) -p(-) log(p(-)), Binary Logarithm

base entrophy는 위의 과정을 통해 0.543을 구할 수 있습니다. 이제 각 속성별 new entrophy를 구해 최종 information gain을 얻는 과정을 살펴보겠습니다. 각 속성별 new entrophy는 자세한 계산과정은 생략한 채, p(+)와 p(-)에 집중하여 보는 것이 좋습니다.

new entrophy를 구하는 과정에서 엔트로피 앞부분에 해당 속성이 선택될 확률(1번에서, E(winter family photo, cartoon)을 구하는 과정에서 E([0+, 4-]) 앞의 p(4/8)를 의미합니다)을 곱하는 부분에 유의하며 이해하면, 쉽게 이해할 수 있을 것입니다. 물론 우리는 직관적으로 "Cartoon Character?" 속성을 먼저 선택하는 것이 유리하다고 판단할 수 있지만, 컴퓨터는 엔트로피 계산 과정을 통해 information gain을 구하는 과정을 거쳐 information gain이 가장 높은 속성인 "Cartoon Character?"를 선택합니다.
이번 포스트에서는 Decision Tree와 ID3 알고리즘을 엔트로피 개념으로 접근해 수학적으로 알아보았습니다. 다음 포스트에서는 SVM(Support Vector Machine)에 대해 알아보겠습니다.
'AI > ML' 카테고리의 다른 글
| SVM(Support Vector Machine) 실습 - 농구 선수 포지션 예측 (0) | 2022.01.08 |
|---|---|
| SVM(Support Vector Machine) (0) | 2022.01.07 |
| kNN(k-Nearest Neighbors) 알고리즘 - 농구선수 포지션 예측(2) (0) | 2022.01.03 |
| kNN(k-Nearest Neighbors) 알고리즘 - 농구선수 포지션 예측(1) (0) | 2022.01.02 |
| kNN(k-Nearest Neighbors) 알고리즘 (0) | 2021.12.23 |