2021. 12. 23. 04:30ㆍAI/ML
이 포스트는 허민석님의 유튜브 머신러닝 내용을 정리한 글입니다. 실습 코드는 도서 나의 첫 머신러닝/딥러닝에서 발췌해왔습니다.
앞으로의 포스트에서는 kNN, Decision Tree, SVM, Naive Bayes 등의 ML supervised learning 알고리즘을 알아볼 테며, 이번에는 kNN 알고리즘에 대해 알아보겠습니다.
kNN(k-Nearest Neighbors), 최근접 이웃법 알고리즘은 ML의 supervised learning 중 한 알고리즘으로, supervised learning(지도 학습)은 classification(분류)과 regression(회귀)로 나뉘며 이때 kNN 알고리즘은 주로 classification, 분류를 위해 사용되는 알고리즘입니다. 참고로 kNN 알고리즘의 군집화, labeling 되는 특징 때문에 unsupervised learning의 clustering(군집화)과 헷갈릴 수 있는데, 이미 관측되고 학습된 데이터들이 존재한다는 점에서 차이점이 있습니다.
kNN 알고리즘을 설명할 때 흔히들 "유유상종"이라는 표현을 많이 인용합니다. 유유상종은
"본시 같은 류의 새가 무리 지어 사는 법입니다."
라는 의미의 속담이며 이를 토대로 이해하면 kNN 알고리즘은 k개의 근접한 새들이 포함된 새의 무리를 찾는 알고리즘입니다.
예를 들어 영화 스파이더맨: 노 웨이 홈이 액션 영화에 포함되는지, 로맨스 영화에 포함되는지 알아보고자 합니다. 우리는 이미 많은 액션 영화와 로맨스 영화를 보고서 해당 영화들의 스킨십 횟수와 싸우는 횟수를 데이터화 했다고 하겠습니다. 이를 토대로 그린 아래의 그래프에서 X축은 skinship count, Y축은 fight count, 로맨스 영화는 x, 액션 영화는 o, 스파이더맨은 *입니다.

먼저, 그림의 1과 2를 보겠습니다. 우리는 직관적으로 1은 Action movie, 2는 Romance movie의 범주에 들어갈 것임을 예측할 수 있으며 실제 학습에서도 동일한 예측이 나올 것입니다. 하지만 * 모양의 스파이더 맨을 보면, 어떤 이들은 skinship count만 보면 Romance movie로 분류해야 한다고 보는 반면 다른 이들은 fight count에 따라 Action movie로 분류해야 한다고 볼 수도 있습니다. 이렇듯 새로운 데이터에 대해 분류하고자 할 때는 약속된 분류 기준이 필요하며, 우리는 kNN 알고리즘을 사용하여 해결할 수 있습니다.
먼저 최근접점 k를 정해야 합니다. 이때 정하는 k는 "분류할 새로운 데이터(*)로 부터 원을 그렸을 때 포함되는 데이터의 수"로 이해하는 것이 좋습니다. k는 1 이상의 수로, 동률을 방지하고자 보편적으로 홀수를 사용합니다. 실제 k = 1에서부터 k 값을 늘려가며 데이터 *를 기준으로 하는 원을 그려보겠습니다.

k = 1일 때입니다. *를 중심으로 하고 근접점이 하나가 포함되도록 원을 그렸을 때, 스파이더 맨은 액션 영화로 분류될 것입니다.
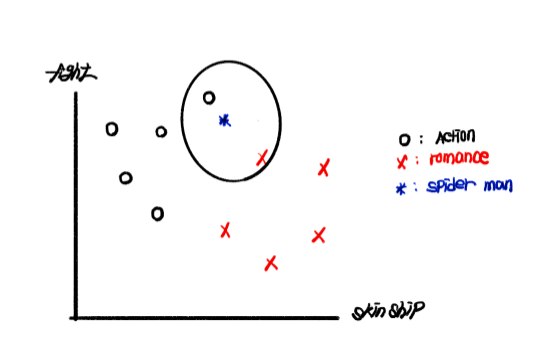
k = 2일 때, 원안에 포함되는 데이터가 각각 하나씩 나와 문제가 발생합니다. 물론 거리상 가까운 데이터(직관적으로는 액션 영화 데이터가 로맨스 영화 데이터에 비해 더 가까워 보입니다)의 분류를 따르거나 랜덤 값을 주어 선택하는 방법도 있지만, 보편적으로는 지향하지 않기 때문에 미리 언급했던 것처럼 홀수를 선택하는 것이 좋습니다.

최종적으로 정한 k의 값을 3으로 했을 때 원 안에 포함되는 데이터는 액션 영화 2, 로맨스 영화 1로, 스파이더맨은 액션 영화로 분류될 것입니다. 이때 처음 드는 의문점이 몇 가지 있을 것입니다. 먼저 "k의 값이 1일 때와 3일 때, 결국 스파이더 맨은 액션 영화로 분류될 것인데 k를 늘려가며 모두 확인해봐야 하는 이유가 있나?" 하는 의문이 들 수도 있습니다. 이는 over fitting(과적합)과 관련이 있으며, over fitting에 대해 궁금하시다면 이전에 over fitting에 대해서 설명한 포스트를 참고하시는 것을 추천드립니다. 다시 돌아와, 극단적인 예시를 들어 k = 1일 때의 문제를 보겠습니다.

우리는 그래프를 봤을 때 스파이더 맨에 근접한 로맨스 영화들이 있지만, 그래도 액션 영화의 범주에 가깝다고 판단할 수 있습니다. 하지만 k = 1로 정한 다음 학습했을 때, 컴퓨터는 최근접한 로맨스 영화의 데이터를 토대로 스파이더 맨을 로맨스 영화로 예측할 것입니다. 이는 원하는 결과가 아닙니다. 심지어 k = 3으로 했을 때도 로맨스 영화로 예측할 것입니다. 이때 적당한 k값은 5라고 할 수 있습니다.

그렇다면 k값이 클수록 좋은 것일까요? 그렇다고 할 수는 없습니다. k값이 과도하게 크다면, under fitting(과소 적합)의 문제가 발생합니다. 위의 그림에서 학습 데이터들은 액션 영화 6개, 로맨스 영화 7개로 13개입니다. 이때 극단적으로 k = 13(13이 큰 수는 아니지만, 현재 예시에서는 데이터 세트 전체에 해당하는 수입니다)으로 설정한 다음 학습한다면, 학습 데이터 간의 거리가 무시된 채 데이터 수가 많은 로맨스 영화로 예측될 것입니다. 이렇듯 분류기가 학습 데이터들의 특징을 반영하지 못한 채 학습하는 것은 지양해야 합니다. 그렇다면 k는 얼마로 두고서 학습을 진행하는 것이 좋을까요? 물론 데이터들의 수, 데이터 고유의 특징 등에 따라 다르지만 검증 데이터만을 넣어 분류 정확도를 측정한 한 모델에서는 아래의 그래프에서처럼 k는 75 근처에서 괜찮은 정확도를 보입니다. 또한 그래프에서 k가 25 미만 일 때는 over fitting의 문제로 정확도가 현저히 낮으며, 75를 지나면서도 under fitting의 문제로 정확도가 낮아지는 추이를 보이고 있다는 점입니다.

다시 돌아와서 kNN 알고리즘에서 새로운 데이터를 중심으로 원을 그리는 것이 이해에 편하다고 했지만, 정확히는 수학적으로 새로운 데이터로부터의 거리를 토대로 계산됩니다. 이때의 거리는 Euclidean distance(유클리드 거리)로, 이차원에서 피타고라스 정리를 이용해 두 점 사이의 거리를 구할 수 있습니다. 아래 그림을 보겠습니다.

그림에서처럼 스파이더 맨 데이터(*)의 좌표가 (6,6)라고 할 때, 스파이더 맨과 다른 모든 데이터 간의 거리를 계산한 다음 최근접한 데이터들이 순서대로 k가 됩니다. 그림에서는 (5,7) 좌표의 액션 영화와의 거리가 √2로 최근접 데이터이며 다음으로는 (7,3) 좌표의 로맨스 영화(√10), 다음으로는 (3,4) 좌표의 액션 영화(√13)입니다. 이렇듯 실제 컴퓨터 연산에서는 거리를 기반으로 계산되어 최근접 k개만큼의 데이터 비를 토대로 예측 및 분류합니다. 따라서 kNN 알고리즘은 거리 기반 분류 분석 모델 알고리즘이며 굉장히 쉽고 직관적으로 이해할 수 있기 때문에 많이 사용됩니다.
사실 kNN 알고리즘은 게으른 학습으로도 불리는데, 현재 데이터 분포를 토대로 학습하기 때문에 단순하고 효율적이며 훈련 단계가 빠르고 유클리드 거리 기반으로 수치 데이터 분류 작업에 높은 성능을 보인다는 장점이 있지만, 따로 모델을 생성하지 않기 때문에 새로운 데이터와 분류되는 군집 사이의 연관성을 명확히 알기 어려우며 k를 적절히 선택하지 못했을 때는 원치 않은 예측값이 나오며 그다음 예측에도 영향을 미칠 수 있다는 단점이 있습니다. 또한 명목 데이터 및 누락 데이터들에 대한 추가 처리 작업이 요구되며 데이터가 많아지면 분류 단계에서 시간이 오래 걸릴 수 있습니다. 이렇듯 여느 알고리즘에서처럼 장점과 단점을 모두 가지고 있지만 kNN 알고리즘은 현재에도 이미지 처리, 얼굴 인식, 추천 시스템, 글자 인식 등 다양한 분야에서 종종 쓰이며 유용한 알고리즘입니다.
'AI > ML' 카테고리의 다른 글
| SVM(Support Vector Machine) 실습 - 농구 선수 포지션 예측 (0) | 2022.01.08 |
|---|---|
| SVM(Support Vector Machine) (0) | 2022.01.07 |
| kNN(k-Nearest Neighbors) 알고리즘 - 농구선수 포지션 예측(2) (0) | 2022.01.03 |
| kNN(k-Nearest Neighbors) 알고리즘 - 농구선수 포지션 예측(1) (0) | 2022.01.02 |
| Decision Tree + ID3 알고리즘 (0) | 2021.12.24 |