2020. 6. 17. 01:00ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.

Vanishing gradient 현상을 해결하기 위한 방법으로 저번 포스트에서 알아 본 ReLU에 이어 이번 포스트에서는 weight을 적절히 초기화하는 방법에 대해 알아보겠습니다. Hinton교수님은 기존의 방법으로 딥러닝 학습이 잘 되지 않았던 이유로 weight을 초기화하는 방법이 적절하지 않았다고 지적하였는데("We initialized the weights in a stupid way"), 그렇다면 먼저 weight을 적절한 방법으로 초기화하지 않았을 때 생기는 문제에 대해 알아보겠습니다.
가장 좋은 예시로는 weight을 모두 0으로 초기화했을 때입니다. 이해를 위해 저번 포스트의 Backpropagation 모형을 다시 보겠습니다.

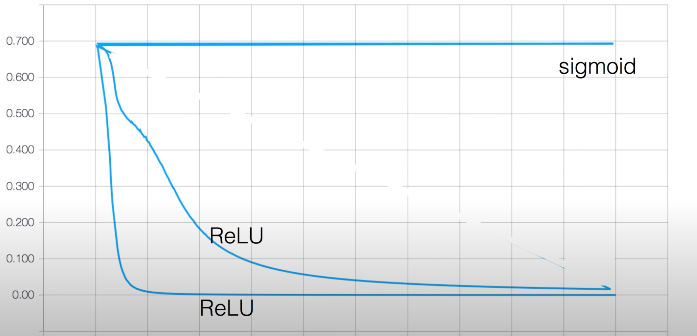
모형을 살펴보면 g = wx일 때 x가 f에 미치는 영향을 알기 위해 ∂f / ∂x를 chain rule에 따라 미분했을 때 ∂g / ∂x = w가 0으로 초기화되어있기 때문에 0의 값을 갖습니다. 따라서 x값에 상관없이 ∂f / ∂x = 0으로 x 그리고 x 이전의 레이어들이 f에 미치는 영향(미분 값)이 모두 0이 됩니다. 따라서 w를 0으로 초기화했을 때는 Vanishing gradient 현상을 피할 수 없습니다. 또 아래의 그래프를 보면 활성화 함수로 ReLU를 사용하였을 때도 cost가 줄어드는 속도가 다른 것을 볼 수 있는데, 이는 weight값을 어떻게 초기화했느냐에 따라 차이가 납니다.
weight을 초기화하는 방법에 대한 연구가 이루어지던 도중, 2006년 Hinton 교수님의 논문 " A Fast Learning Algorithm Deep Belief Nets - Restricted Boltzmann Machine(RBM)"에서 weight을 적절한 값으로 초기화하는 방법에 대해 설명하였는데, 이 논문에서 나온 방법이 바로 Restricted Boltzmann Machine(RBM)이며, 이 방법으로 weight을 초기화한 네트워크를 Deep Belief Nets(DBN)이라고 합니다. 지금은 RBM보다 훨씬 쉽고 좋은 방법들도 많이 나왔지만, RBM은 weight을 초기화하는 방법들에게 초석을 마련했다고 볼 수 있으므로 꼭 알아두길 바랍니다. 그렇다면 RBM에 대해 알아보겠습니다.
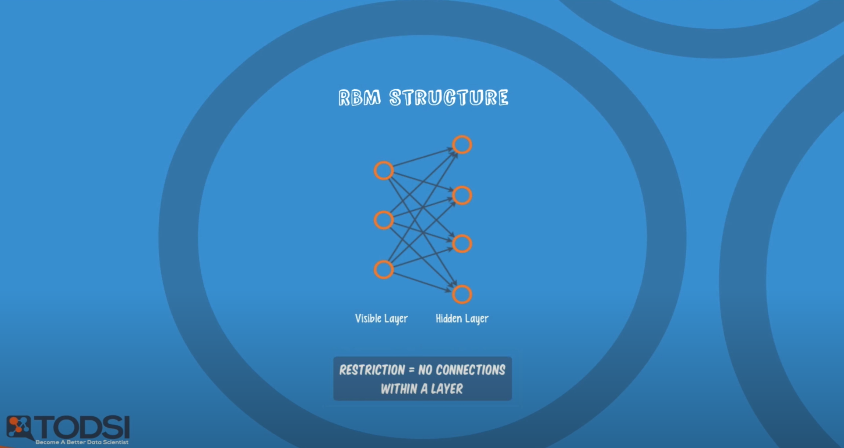
먼저 RBM의 구조를 보겠습니다. RBM은 두 개의 레이어로 구성되어 있으며 따라서 RBM 구조 그 자체로 딥 네트워크는 아니지만, RBM은 딥 네트워크 중 하나인 DBN을 구성하는 요소입니다. 두 개의 레이어는 Visible Layer와 Hidden Layer이며 위의 그림에서 Visible Layer에서 Hidden Layer로 연결되어있는 것을 봐서 우리는 이전에 배운 내용을 토대로 Visible Layer를 Input Layer라고 예측할 수 있을 것입니다. 실제로 Visible Layer는 Input Layer와 동일하며 위의 방식으로 차례대로 Input Layer - Hidden Layer , Hidden Layer - Hidden Layer, Hidden Layer - Output Layer와 같은 구조로 두 개의 레이어로 구성된 RBM들을 연결하여 DBN을 구성합니다. RBM에서 R은 Restricted(제한되어 있다는 뜻입니다)로, 그림에서도 확인할 수 있듯이 모든 Input Layer의 노드들과 Hidden Layer의 노드들이 서로 연결되어 있지만 같은 레이어의 노드들끼리는 연결되어 있지 않다는 것을 의미합니다. Input Layer의 노드들에서 각각 초기화 된 weight와 bias를 연산하여(Input Layer 하나의 노드를 x라고 할 때, 연산 결과는 wx + b입니다.) 활성화 함수에 넣어 나온 확률값에 따라 입력을 전달할 지(1), 전달하지 않을 지(0)를 결정합니다. 이제 RBM 구조에서 weight를 정하는 방법을 보겠습니다.

먼저 Input Layer의 하나의 노드를 x라고 할 때, Forward 과정에서는 x를 weight과 곱한 값 X를 Hidden Layer의 노드에 전달합니다. 이후 weight는 그대로 둔 채 Hidden Layer의 X를 다시 Backward하여 Input Layer에 전달하며 이 값을 x̂라고 합니다. 이 때 x와 x̂의 차가 최소가 되는 weight를 최적의 weight로 설정합니다. 이 때 Forward와 Backward 과정을 각각 auto encoder, auto decoder라고 합니다. 이후 인접한 다음 레이어와 weight을 학습하는 과정을 반복하는데, 이 과정을 Pre-training이라고 합니다. 반복해가며 마지막 레이어까지 Pre-training 과정이 끝난 네트워크에 데이터를 가지고 학습하는 것을 Fine Tuning이라고 합니다. Fine Tuning이란 기존에 학습되어져 있는 모델을 기반으로 새로운 목적에 맞게 변형하고 이미 학습된 weight으로 부터 학습을 업데이트 하는 방법을 말합니다. 위에서는 Pre-training에 의해 학습되어진 모델과 weight을 기반으로 학습을 업데이트하는 것을 의미합니다. 사실 지금까지의 설명만으로는 RBM의 학습과정을 확실히 이해하기 어려웠습니다. Auto encoder/decoder과정을 예시를 들어 설명하고 싶었지만 아직은 지식이 부족하여 정확히 이해하지 못하여 설명해드리지 못한 점 죄송합니다. 다만 혹시나 RBM 학습 과정에 대해 궁금하신분들은 다음의 링크 PDF를 통해 한번 확인해주시길 바랍니다. 이후 RBM에 대한 확실한 이해 이후 포스트를 업데이트하겠습니다. 아래의 Pre-training과 Fine tuning 그림을 보고 넘어가겠습니다.


RBM의 학습 과정에 대한 정확한 이해 없이 다음 스텝으로 넘어갈 수 있는 이유는 RBM 이후 2010년과 2015년 Xavier initialization과 He's initialization의 등장입니다(줄여서 Xaiver, He's라고 하겠습니다). Xavier는 입력과 출력의 수에 맞추어 weight의 초기화 값을 정하는 방법입니다. He's는 Xavier의 방법을 좀 더 개선한 것이며 이 방법으로 imagenet의 오류를 3% 미만으로 줄어들게 했습니다. 두 방법은 입력의 수를 fan_in, 출력의 수를 fan_out이라고 했을 때 아래의 코드와 같습니다.
# Using number of input(fan_in) and output(fan_out)
# Xvaier initialization, 2010
W = np.random.randn(fan_in, fan_out)/np.sqrt(fan_in)
# He's initialization, 2015
W = np.random.randn(fan_in, fan_out)/np.sqrt(fan_in/2)마지막으로 강의에 나온 stackoverflow의 Xavier_init 함수를 소개하며 포스팅을 마치겠습니다. 이번 포스트에서는 weight을 초기화하는 좋은 방법들에 대해 살펴보았습니다. 일전에 말했듯이 Xavier, He's 초기화 방법 등 쉽고 좋은 방법들이 많이 나왔지만, RBM은 이 방법들의 시작이므로 꼭 알아두면 좋다고 생각합니다.
def xavier_init(n_inputs, n_outputs, uniform=True):
"""Set the parameter initialization using the method described.
This method is designed to keep the scale of the gradients roughly the same
in all layers.
Xavier Glorot and Yoshua Bengio (2010):
Understanding the difficulty of training deep feedforward neural
networks. International conference on artificial intelligence and
statistics.
Args:
n_inputs: The number of input nodes into each output.
n_outputs: The number of output nodes for each input.
uniform: If true use a uniform distribution, otherwise use a normal.
Returns:
An initializer.
"""
if uniform:
# 6 was used in the paper.
init_range = math.sqrt(6.0 / (n_inputs + n_outputs))
return tf.random_uniform_initializer(-init_range, init_range)
else:
# 3 gives us approximately the same limits as above since this repicks
# values greater than 2 standard deviations from the mean.
stddev = math.sqrt(3.0 / (n_inputs + n_outputs))
return tf.truncated_normal_initializer(stddev=stddev)'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 10-4. 레고처럼 네트워크 모듈을 마음껏 쌓아 보자 (0) | 2020.06.19 |
|---|---|
| 10-3. Dropout과 앙상블 (0) | 2020.06.19 |
| 10-1. Sigmoid 보다 ReLU가 더 좋아 (0) | 2020.06.13 |
| 09-4. XOR 문제 keras로 풀어 Tensorboard로 확인 LAB (0) | 2020.06.13 |
| 09-3. Neural Net for XOR LAB (0) | 2020.06.09 |