2020. 6. 9. 13:30ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.
이번 포스트에서는 실제 텐서플로우 코드로 XOR문제를 딥러닝으로 구현해보겠습니다. 09. XOR문제 딥러닝으로 풀기에서 살펴보았듯이 XOR(배타적 논리합) 문제는 뉴럴 네트워크에서 하나의 perceptron으로 학습하여 해결하는 것은 어렵다는 것을 알고 있습니다. 또한 논리 연산의 결과가 1, 0 두 분류로 나뉘기 때문에 Logistic regression의 sigmoid function을 적용하여 해결하는 것이 좋아 보입니다. 따라서 이번 코드는 기본적으로 05-2. Logistic Regression LAB의 코드의 함수들을 이용하며 다만 차이점은 레이어가 둘 이상이라는 점입니다. 아래에서 코드를 보며 다시 이야기하겠습니다.
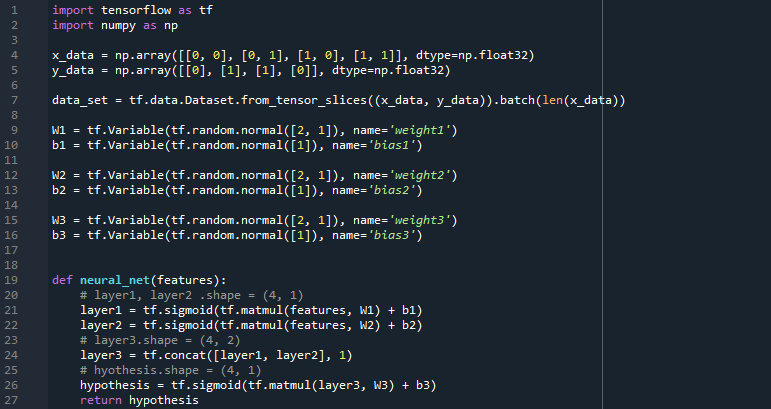
line 1 - 27을 살펴보겠습니다. 사실 이 부분이 이번 코드의 핵심입니다. 우리는 이미 XOR문제의 입출력을 알고 있으므로 x_data와 y_data를 정하는 것에는 무리가 없을 것입니다. x_data와 y_data를 쌍으로 갖는 data_set을 선언하는 것도 이전 LAB포스트들에서 익숙하게 보았을 것입니다. 이제 line 11 - 18을 살펴보겠습니다. 우리는 이전 포스트 09. XOR문제 딥러닝으로 풀기에서 세 개의 레이어를 활용하여 XOR문제를 풀 수 있음을 이미 알고 있기 때문에 세 레이어의 weight와 bias를 따로 선언합니다. x_data의 요소들이 1x2 배열이므로 이후의 matmul연산을 생각하여 임의의 weight값을 갖는 2x1배열을 선언하는 것을 볼 수 있습니다. 문제 해결에서 핵심인 MLP, 다층 퍼셉트론(둘 이상의 레이어를 말합니다)을 구현한 것이 바로 line 21 - 27의 neural_net함수입니다. neural_net함수는 세 개의 layer를 선언하며 layer1과 layer2의 연산을 합친 layer3을 토대로 hypothesis를 구하여 리턴하는 것을 볼 수 있습니다. 조금 더 자세하게 살펴보면 layer1과 layer2는 각각 features(x_data)와 W1, W2를 곱한 뒤 b1, b2를 더하여 sigmoid function에 넣어 값에 따라 1 혹은 0의 값을 가질 것이며 이 layer를 tf.concat 함수를 이용하여(tf.concat 함수에 대한 자세한 설명은 링크의 블로그에서 확인하실 수 있습니다. 블로그에서 손 그림으로 tf.concat의 과정을 표현한 것을 보면 확실히 이해하실 수 있을 것입니다.) layer3에 넣습니다. line 25에서는 layer3를 W3와 연산할 수 있도록 적절한 형태로 변환하지만, 이번의 경우는 line 24에서 tf.concat으로 합쳐지며 이미 1x2 배열이기 때문에, 삭제해도 무방할 것으로 생각합니다. 이후 layer3을 연산한 결과를 hypothesis에 넣어 리턴하는 동작을 하고 있습니다. 우리는 지금껏 하나의 레이어(사실 여태 우리는 레이어를 표현하지 않았습니다.)만을 이용하여 머신 러닝의 기본적인 개념들을 구현해보았기 때문에 위의 neural_net 함수가 어색하게 느껴질 수 있습니다. 하지만 위의 코드처럼 MLP(다층 퍼셉트론)를 이용하여 학습하는 것이 딥러닝의 시작입니다. 저는 이번 포스트를 시작으로 비로소 딥러닝에 첫발을 내딛게 되었다고 생각합니다. 아래의 코드들은 모두 이전의 Logistic Regression LAB에서 배웠으므로 짧게 살펴보고 넘어가겠습니다.

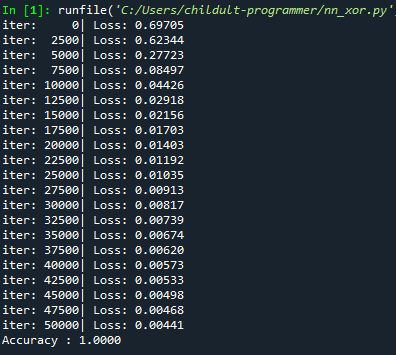
먼저 line 35에서 learning rate를 0.03으로 설정한 것은 SGD의 디폴트 값인 0.01로 학습해보았을 때 학습이 잘 되지 않아 3배를 올린 0.03으로 설정하였으며 3배를 올린 이유는 이전 Andrew Ng 교수님의 머신러닝 강의에서 배운 기억으로 적용해보았으나 정확히 3배씩 올리는 것이 맞는지는 다시 확인해봐야겠지만 learning rate를 0.03으로 두고 학습하였을 때는 보다 나은 결괏값을 얻었습니다. (물론 매 실행마다 W와 b가 임의로 변하기 때문에 learning rate의 증가가 큰 변화를 가져왔는지는 단언할 수는 없습니다.) 아래는 코드 실행 결과입니다. 50000번이나 반복하기 때문에 실행에 꽤나 오랜 시간이 걸렸지만 원하는 결과를 얻을 수 있었습니다. 다만 iter 0 - 2500에서 cost의 변화가 뚜렷하지 않았으나 iter 2500 - 5000에서 cost가 급격하게 떨어진 것은 다소 의아합니다. 이 부분은 다음 포스트에서 알아볼 Tensorboard를 활용해 시각적으로 살펴보겠습니다.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 10-1. Sigmoid 보다 ReLU가 더 좋아 (0) | 2020.06.13 |
|---|---|
| 09-4. XOR 문제 keras로 풀어 Tensorboard로 확인 LAB (0) | 2020.06.13 |
| 09-2. 딥네트워크 학습 시키기 (Backpropagation) (0) | 2020.05.21 |
| 09. XOR 문제 딥러닝으로 풀기 (0) | 2020.05.11 |
| 08. 딥러닝의 기본개념, 역사 (0) | 2020.05.08 |