2020. 6. 13. 20:55ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.
이번 포스트에서는 뉴럴 네트워크에서 활성화 함수(Activation function)의 한 종류인 sigmoid의 문제점을 인지하고 이를 해결하기 위해 나온 ReLU에 대해 알아보겠습니다. 쉬운 이해를 위해 뉴럴 네트워크의 한 예를 들어보겠습니다.


위는 뉴럴 네트워크의 한 예시입니다. input Tensor가 x1과 x2일 때 Output이 shape=(1,)의 Tensor Y로 고정되어있는 점을 제외하면 Input Layer와 Output Layer 사이의 Hidden Layer에는 어떤 형태로의 연결이든 상관없습니다. 문제에서는 Weight을 [2, 4] -> [4, 3] -> [3, 1]로 연결하여 Y를 얻고 있습니다. 실제로 위의 코드를 완성하여 학습하면 원하는 Y를 얻을 수 있습니다. 하지만 이번에는 9개의 Hidden Layer로 연결되어 있는 경우를 살펴보겠습니다. 실제 W1 - W9, b1 - b9를 작성하여 텐서보드에서 보면 아래와 같이 Input Layer와 Output Layer를 제외한 9개의 Hidden Layer(layer2 - layer10)로 연결되어 있는 모습을 볼 수 있습니다.
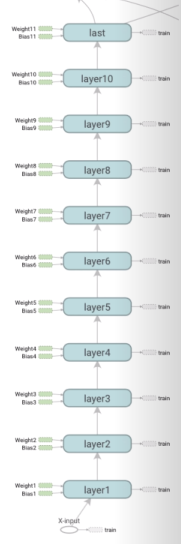
코드를 완성하여 위의 모델을 학습하면 어떤 결과가 나올까요? 불행하게도 원하는 결과를 얻지 못하였습니다.(실행 시 결과 예시는 영상에 있습니다. ) 우리는 Hidden Layer가 많아질수록 많은 학습으로 더욱 정확한 예측을 얻을 것이라 기대했지만, 실제 정확도는 0.5에 그쳤습니다. 아래 TensorBoard에서 cost와 accuracy의 그래프를 보면 cost가 일정 수준으로 떨어졌다가 더 이상 줄어들지 않는 모습을 보이며 accuracy 또한 0.5를 유지하다가 0.75 수준으로 올라갔다 내려갔다를 반복하는 모습을 보입니다.

왜 이런 결과를 보일까요? 답은 학습 과정인 Backpropagation에 있습니다. 09-2. 딥네트워크 학습시키기 (Backpropagation)의 모형 2.1을 보겠습니다.

위의 모형에서 y는 바로 이전 레이어의 값을 sigmoid한 0 ~ 1 사이의 값을 가집니다. 예를 들어 y가 바로 이전 레이어의 값을 sigmoid한 0.01의 값을 가질 때, x를 미분한 df/dx는 (dg/dx) * (df/dg) = 0.01 * (df/dg)의 값을 가집니다. 이런 식으로 앞으로 계속 올라가다 보면 미분 값은 0.01 * 0.03 * 0.06... 와 같이 매우 작은 값을 가질 것입니다. 노드를 미분한 값은 노드가 결과에 미치는 영향을 의미하기 때문에 실제로 노드가 Output Layer에서 멀어질수록 결과에 영향을 작게 미칠 것입니다. 이는 0과 1 사이의, 1보다 작은 수만을 갖는 sigmoid의 특성상 앞의 노드로 갈수록 값이 줄어들기 때문입니다. 물론 위의 모형에서 연산자가 *가 아닌 +였다면 df/dx는 (dg/dx) * (df/dg) = 1 * (df/dg)로 (df/dg)에 따라 미치는 영향이 바뀌었을 수도 있습니다.
또한 아래 sigmoid의 도함수의 최댓값이 0.25인것을 생각하면 학습망이 깊어질수록 미치는 영향이 줄어들 것임을 생각할 수 있습니다.

이러한 현상을 Vanishing gradient라고 합니다. Vanishing gradient는 뉴럴 네트워크에서 Backpropagation으로 학습하는 도중 활성화 함수를 sigmoid로 설정해 0과 1 사이의 값이 지속적으로 곱해지는 이유로 Gradient 항이 사실상 사라져 학습망이 깊어질수록 이전의 노드들이 결과에 미치는 영향이 급격히 줄어드는 상황을 말합니다. 아래 그림을 보면 한눈에 이해하실 수 있을 것입니다.

그렇다면 Vanishing gradient가 활성화 함수(Activation function)를 sigmoid로 설정했기 때문에 일어남을 알았으므로 이제 우리는 새로운 형태의 활성화 함수가 필요합니다. 이런 필요에 의해 나온 활성화 함수가 바로 ReLU(Rectified Linear Unit)입니다. 먼저 ReLU와 ReLU의 도함수 그래프는 아래와 같습니다.
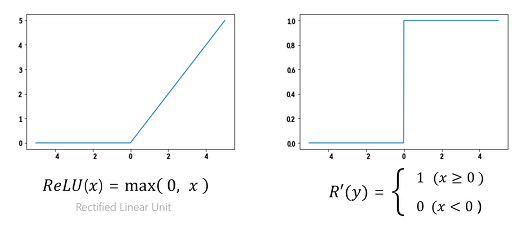
ReLU의 핵심은 0보다 작은 경우는 0을 반환하고 0보다 큰 경우에는 값을 그대로 갖는다는 점입니다. 따라서 최댓값이 1보다 큰 값도 가능하기 때문에 Vanishing gradient를 방지하고 학습이 빠릅니다. 또한 sigmoid와는 달리 도함수가 0 또는 1의 값만을 갖기 때문에 컴퓨터 자원 측면에서도 경제적이라는 장점이 있습니다. 실제로 TensorBoard에서 학습 결과를 확인해보면 accuracy와 cost의 값이 빠르게 변하는 것을 확인할 수 있습니다.

ReLU 함수 외에도 Tanh, Leaky ReLU, PReLU, Maxout 등의 다양한 활성화 함수가 있습니다. 각 활성화 함수들을 때에 따라 적절히 사용하면 좋은 학습 결과를 얻을 수 있습니다. 짧게 짚고 넘어가면 Tanh은 sigmoid의 중심을 0으로 맞추어 최솟값과 최댓값의 범위를 -1에서 1 사이로 변경한 것이며 Leaky ReLU는 0보다 작은 값이 0이 아닌 0 0보다 작은 값, 단 적당히 작은 값을 갖도록 ReLU = max(0, x)에서 Leaky ReLU = max(0.1x, x)의 형태로 바꾼 것입니다.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 10-3. Dropout과 앙상블 (0) | 2020.06.19 |
|---|---|
| 10-2. Weight 초기화 잘해보자 (0) | 2020.06.17 |
| 09-4. XOR 문제 keras로 풀어 Tensorboard로 확인 LAB (0) | 2020.06.13 |
| 09-3. Neural Net for XOR LAB (0) | 2020.06.09 |
| 09-2. 딥네트워크 학습 시키기 (Backpropagation) (0) | 2020.05.21 |