2020. 5. 11. 03:35ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.
우리는 저번 포스트에서 딥러닝 역사에 대해 알아보며, 1950년 후반대 인공지능에 대한 높은 기대감에 찬물을 끼얹은 첫 번째 문제인 XOR모델 분류 문제에 대해 알아보았습니다. 먼저 XOR모델은 AND, OR모델과는 다르게 linear 한 방법으로는 결과를 예측할 수 없습니다. 하지만 이후 Marvin Minsky 교수님이 MLP(다층 퍼셉트론)를 이용하여 문제를 해결할 수 있다고 발표하였으며 시간이 지나 1986년 Hinton 교수님의 Backpropagation 알고리즘이 발표되며 문제가 완벽히 해결되었습니다. 이번 포스트와 다음 포스트에서는 XOR모델을 분류하는 문제를 딥러닝으로 풀어보며 Backpropagation 알고리즘까지 알아보겠습니다.

먼저 위의 그림 1.1의 그래프(좌)를 먼저 보겠습니다. X1을 x축, X2를 y축으로 놓았을 때 XOR(배타적 논리합)은 X1과 X2, 2개의 명제 가운데 1개만 참일 경우 참으로 판단하는 논리 연산입니다. 그래프에서 알 수 있듯이 linear 한 방법으로는 +(1)와 -(0)를 분류할 수 없습니다. 이를 해결하기 위해 뉴럴 네트워크에서 MLP, 즉 하나의 퍼셉트론이 아닌 여러 개의 퍼셉트론을 활용하여 문제를 푸는 방법이 발표되었습니다. 그러면 이제 XOR모델 분류 문제를 풀어보겠습니다. 먼저 문제를 풀면서 나오는 Weight와 bias를 설정하는 것은 다음 포스트에서 알아볼 것이므로, 이번 포스트에서는 일단 hypothesis(Wx + b)의 W와 b를 미리 적절한 값으로 정하고 진행하겠습니다. 문제 해결 모형은 아래 그림 2.1과 같습니다.

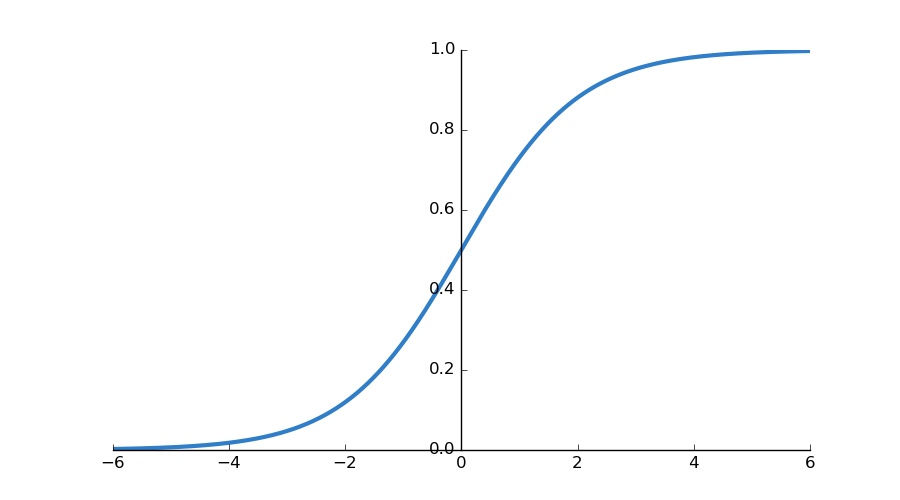
기본적인 문제해결 과정은 다음과 같습니다. 본 문제는 두 명제 간의 논리 연산의 결과가 1이냐 0이냐, 두 경우로 분류되기 때문에 Logistic regression의 sigmoid function을 적용하여 값을 구합니다. 이때 sigmoid 과정에서 Decision boundary 값이 0.5보다 크면(양수) 1, 작으면(음수) 0으로 분류합니다. H(x) = Wx + b로 놓고 정해진 W와 b에 (X1, X2)의 모든 조합에 대한 Y1과 Y2를 다시 perceptron에 넣어 Ŷ를 구하여 XOR 모델의 Y와 비교하여 평가합니다. 그림 1.1의 표(우)의 위에서부터 (1), (2), (3), (4)로 놓고 각각의 경우에 대해 직접 계산해보겠습니다.




식을 자세히 살펴보면, 계산이 어렵지 않음을 알 수 있습니다. H(X) = XW + b에 맞춰 행렬 곱과 bias를 더한 값을 sigmoid에 넣어 1과 0을 구분하고, 이 값을 토대로 Ŷ를 구해 Y와 비교해 같은지, 같지 않은지를 판단하고 있습니다. 그림 2.1에서 박스는 perceptron(gate, unit)을 의미하며 perceptron이 둘 이상 쓰이는 것으로 우리는 모형이 MLP(다층 퍼셉트론)를 이용하여 문제를 해결하고 있음을 알 수 있습니다. 이제 계산을 통해 W, b값이 적절하고 모형이 옳다는 결과가 나왔기 때문에, 그림 2.1의 모형을 조금 다르게 표현해보겠습니다.

우리는 이러한 모형의 순서대로, 즉 뉴럴 네트워크 모델의 입력층부터 출력층까지 순서대로 변수들을 계산하고 저장하는 것을 forward propagation, 순전파라고 부르겠습니다. 다시 설명하면 위 모델은 X1과 X2가 하나의 perceptron을 거쳐 계산되어 Y1과 Y2의 값을 만들고 다시 이 값을 다른 perceptron에 넣어 예측값 Ŷ를 구하는 순서대로 계산되기 때문에 순전파의 전형적인 모델 중 하나입니다. 단순히 순전파는 그 자체로도 의미 있지만, 다음 포스트에 나올 backward propagation(역전파)을 논의할 때 도움이 될 것이기 때문에 미리 알아두는 것이 중요합니다. 마지막으로 모형을 조금 더 변형해보겠습니다. 이전 포스트 06. Softmax classification - Multinomial classificaiton에서 배운 multinomial classification을 활용하여 W와 b를 하나로 묶어 표현하고 이를 식으로 표현하겠습니다. 이러한 방식은 후에 다른 문제에서 X의 개수가 많을 때 단순하게 표현할 수 있다는 장점을 가지고 있습니다.

그림 2.4는 multinomial classification을 활용하여 모형을 단순하게 만들었습니다. 이전의 두 W와 B를 하나의 행렬로 합쳐 연산해 나온 행렬을 K라 두고 다시 perceptron에 넣어 예측값 Ŷ를 구하는 방법으로, 이 과정을 식으로 나타내고 있습니다. 아래의 식은 텐서플로우 코드로 바꾸어도 굉장히 간단히 나타낼 수 있습니다.
# Neural Network(NN)
K = tf.sigmoid(tf.matmul(X, W1) + B1)
hypothesis = tf.sigmoid(tf.matmul(K, W2) + B2)이렇게 우리는 뉴럴 네트워크에서 순전파 알고리즘을 통해 logistic regression의 sigmoid function을 이용해 직접 계산해보며 XOR문제를 해결했습니다. 다층 퍼셉트론을 이용하여 모형을 만들고 이를 간단한 모양으로 표현하기 위해 multinomial classificaiton을 활용하였습니다. 이처럼 앞으로 딥러닝을 배울 때는 이전의 linear regression, softmax classifcation 등 머신러닝의 기본적인 개념이 굉장히 중요함을 느낄 것입니다. 이전 포스트들을 훑어보며 다시 복습해보는 것도 큰 도움이 될 것이며, 혹은 앞으로 개념이 등장할 때마다 링크된 포스트에 들어가 잠깐 개념을 보고 돌아오는 것도 하나의 방법이 될 것입니다. 강의에 직접 소개되지는 않았지만, W와 b는 포스트의 조합 이외에도 많은 조합이 있습니다. 단순히 W에 2배, 3배를 곱하는 것도 하나의 방법입니다. 하지만 적절한 조합을 찾아 설정하는 것이 regulation의 핵심이기 때문에, 적절한 W와 b의 조합을 찾는 것이 매우 중요합니다. 다음 포스트에서는 이번 포스트 마지막 모형에 나온 W1, B1, W2, b2를 training data에서 학습하는 방법인 Backpropagation(역전파)에 대해 알아보겠습니다.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 09-3. Neural Net for XOR LAB (0) | 2020.06.09 |
|---|---|
| 09-2. 딥네트워크 학습 시키기 (Backpropagation) (0) | 2020.05.21 |
| 08. 딥러닝의 기본개념, 역사 (0) | 2020.05.08 |
| 07-2. Model evaluation: Training and test data sets (0) | 2020.05.04 |
| 07-1. Learning rate, Feature scailing, Overfitting, and Regularization (0) | 2020.04.30 |