2020. 3. 31. 01:25ㆍAI/모두를 위한 딥러닝
이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.
이번 포스트에서는 텐서플로우에서 Simple Linear Regression(단순 선형 회귀)과 Cost Function (비용 함수)을 최소화하는 알고리즘인 Gradient descent(경사 하강법)을 어떻게 구현하는지를 간단한 예시를 통해 알아보겠습니다. (들어가기에 앞서 Linear Regression과 Cost Function에 대해 궁금하시다면, 이전 포스트를 참고해주시기 바랍니다.)
· 다음의 Training Data Set을 보겠습니다.
x_data = [1, 2, 3, 4, 5] # Input values
y_data = [1, 2, 3, 4, 5] # Output values
위 데이터는 입력과 출력이 같기 때문에, 우리는 H(x) = Wx + b에서 W와 b가 1, 0이라고 예측할 수 있습니다. 다음의 텐서플로우 코드로 확인해보겠습니다.
아래의 코드는 Spyder(tensorflow)에서 작성되었습니다. Anaconda Prompt에서 tensorflow를 설치했다면 Anaconda Navigator에서 tensorflow Spyder을 다운로드하실 수 있습니다.
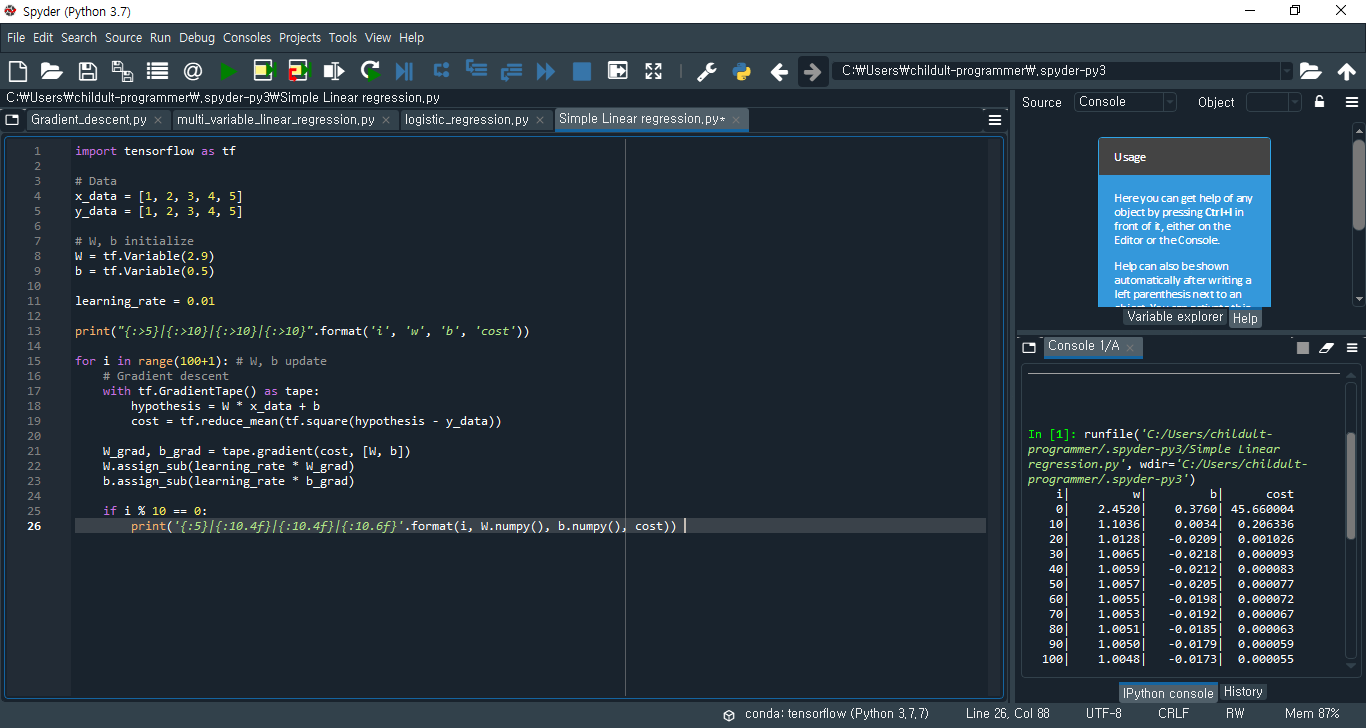

1.1. 입출력 데이터(x_data, y_data)를 주고 Variable()로 변수 W와 b의 초기값을 임의로 지정해주었습니다. 이 데이터들로 그래프에 Data와 H(x)를 표시해보겠습니다. (H(x) = 2.9x + 0.5)

위 그래프에서 보이듯이, W와 b가 각각 2.9와 0.5일 때 오차가 꽤나 큰 것으로 보입니다. 실제로 결괏값에서 초기 cost는 45.66으로 굉장히 큰 것을 알 수 있습니다.

2.1. 상수 learning_rate를 지정해주었습니다.
learning_rate(학습 속도)란, W와 b의 미분 값(W_grad, b_grade)을 얼마만큼 반영할지를 결정하는 값입니다. 주로 0.001, 0.00001과 같은 매우 작은 값을 사용하며 learning_rate가 클수록 변화가 빠르며, learning_rate가 작을수록 변화가 느리다고 봅니다. 추후에 다시 나오지만, 꼭 변화가 빠르다고 해서 결과를 빨리 볼 수 있는 것은 아닙니다.

3.1. 일반적으로 텐서플로우에서 Gradient descent 알고리즘은 GradientTape()을 이용하여 구현합니다. GradientTape()은 with블록 내 변수들(W, b)의 변화를 tape에 저장하며, 이후 우리는 tape.gradient() 메서드를 호출해 변수들의 미분 값을 구하여 변수를 업데이트할 수 있습니다.
3.2. Cost Function을 구현한 cost = tf.reduce_mean(tf.square(...))을 살펴보겠습니다. 먼저, 이전 포스트에서 배운 Cost Function은 아래와 같습니다. 그럼 각각의 함수가 어떤 기능을 하는지 알아보겠습니다.
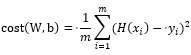
tf.square()은 인자를 제곱한 값을 반환하는 메서드로, tf.square(hypothesis - y_data)는 오차를 제곱한 값을 반환합니다. 또 tf.reduce_mean()은 한 차원 아래의 평균을 구하는 메서드로, tf.square()에서 반환된 값의 평균을 구합니다. 이제 우리는 텐서플로우에서 이 두 메서드를 활용해 오차 제곱의 평균(MSE)을 구하는 cost 함수를 구현할 수 있습니다.

4.1. W_grad, b_grad = tape.gradient(cost, [W, b])는 cost에 대해 tape에 저장된 변수(W, b)를 미분한 값을 튜플로 반환하여 W_grad, b_grad에 순서대로 저장합니다.

5.1. W.assign_sub(Args) 메서드는 파이썬의 W -= Args와 같은 개념으로, 인자를 뺀 값을 다시 할당해주는 역할을 합니다. 따라서 이 메서드를 사용해서 우리는 W, b에서 이전에 구한 W_grad, b_grad에 learning_rate를 곱한 값을 빼서 W와 b에 할당해주는 과정을 통해 W와 b를 업데이트해줍니다. (W -= W.grad * learning_rate, b -= b.grad * learning_rate)

6.1. W, b, cost 값의 변화의 추이를 보기 위해 if문을 사용해 i가 10의 배수일때 값을 출력하도록 했습니다.
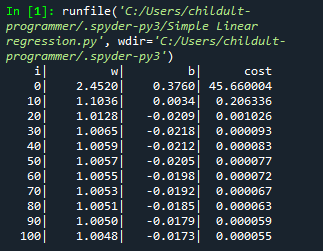
6.2. 출력값을 보면 W는 2.45에서 1.00으로 점차 1에, b는 0.37에서 -0.01로 점차 0에, cost는 45.6에서 0.00으로 0에 수렴하는 것을 알 수 있습니다. 이 데이터들로 그래프 1.2. 에 추가해 i = 100일 때의 그래프를 그려보면 H(x)가 Training set에 가까워진 것을 확인할 수 있습니다.

이번 포스트에서는 텐서플로우에서 Linear Regression(선형 회귀)을 구현하며 Cost Function(비용 함수)와 텐서플로우 문법에 대해 알아보았습니다. 다음 포스트에서는 비용을 최소화하는 방법에 대해 알아보겠습니다.
'AI > 모두를 위한 딥러닝' 카테고리의 다른 글
| 03-1. How to minimize cost - Gradient descent LAB (3) | 2020.04.04 |
|---|---|
| 03. How to minimize cost - Gradient descent (0) | 2020.04.03 |
| 02-1. 텐서플로우(TensorFlow)란? / 텐서플로우 설치 (1) | 2020.03.26 |
| 02. Simple Linear Regression (1) | 2020.03.23 |
| 01. 기본적인 Machine Learning 의 용어와 개념 설명 (0) | 2020.03.22 |