02. Simple Linear Regression

이 포스트는 모두를 위한 딥러닝 - Tensor Flow를 정리한 내용을 담았습니다.
누구나 이해할 수 있는 수준으로 설명하고자 하였으며 LAB의 코드는 TF2.0에 맞추어 재작성되었습니다.

·Linear Regression (선형 회귀)

- Regression 이란?

우리는 이전 포스트 01. 기본적인 Machine Learning의 용어와 개념 설명의 지도 학습 예시인 부동산 가격 예측을 통해 Regression에 친숙해져 있을 수 있습니다.

실제로 Regression은 통계학자이자 인류학자였던 Sir Francis Galton이 말한 "Regression toward the mean", 즉 "전체의 평균으로 되돌아간다"는 것을 의미합니다.

자세히 말하자면, 어떤 데이터들이 굉장히 크거나 작을지라도 전체적으로 이 데이터들은 전체 평균으로 회귀하려는 특징이 있다는 의미의 통계적 원리입니다.

 

- Linear Regression (선형 회귀)

Linear Regression는 쉽게 "데이터를 가장 잘 대변하는 직선의 방적식을 찾는 것"입니다.

y = ax + b는 데이터들을 가장 잘 대변하는 직선입니다.

위 그림에서 점으로 표현된 많은 데이터들을 가장 잘 대변하는 직선은 y = ax + b입니다.  즉, Linear Regression은 이 직선 방정식의 a값과 b값을 구하는 것을 목적으로 합니다.

 

- Hypothesis

+) 아래에서부터는 이전 설명에서의 y = ax + b를 H(x) = Wx + b로 표현하겠습니다.            (H(x)는 Hypothesis, W는 Weight, b는 bias로 정해서 표현하였습니다.)

아래의 표는 (X, Y)를 쌍으로 갖는 training data set의 한 예시입니다. 

 

X	Y
1	1
2	2
3	3

 

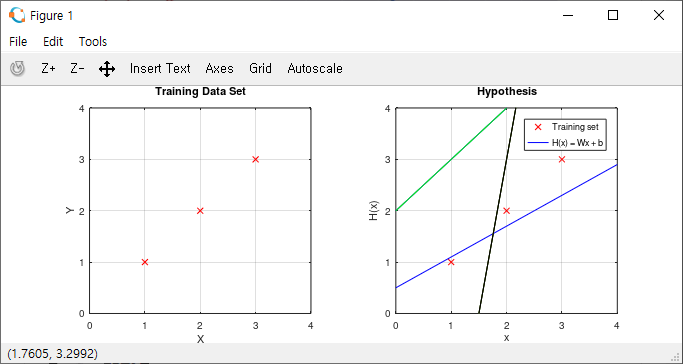
위의 표에 나온 (X, Y) 데이터를 그래프에 표시하면 아래 왼쪽의 "Training Data Set"으로 표현할 수 있습니다.

아래 오른쪽의 Hypothesis, 직선들 중 데이터를 가장 잘 대변하는 직선은 파란색이며, 우리는 이 직선을

H(x) = Wx + b로 정할 것입니다. (물론 이 데이터를 가장 잘 대변하는 직선은 H(x) = x라는 것이 직관적이지만, 실제로는 훨씬 많은 (X, Y) 쌍의 데이터가 존재한다는 전제 하에 있습니다.)

따라서 데이터를 가장 잘 대변할 수 있는 H(x)의 W와 b를 정하는 것이 Linear Regression의 목적입니다.

그래프 1.1. Training Data Set(좌), Hypothesis(우), Octave로 프로그래밍 되었습니다.

 

 

- Cost / Cost function

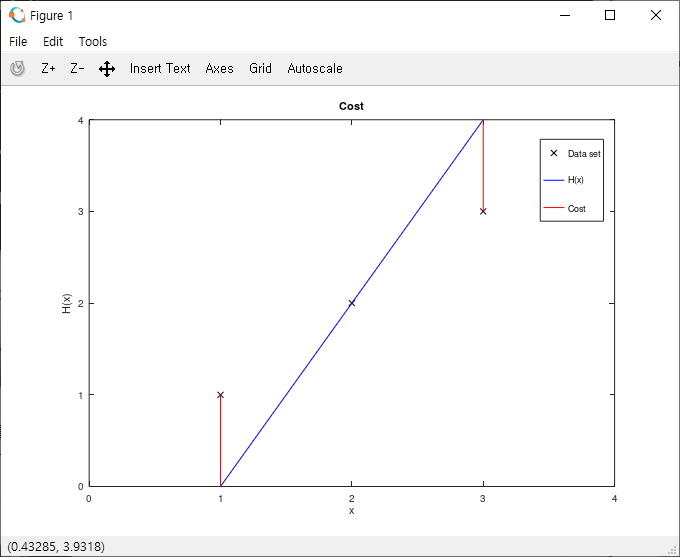
Cost는 아래 그래프(1)에서 빨간 선으로 표현되어있듯 Hypothesis(H(x))와 실제 데이터(y)의 차이를 말합니다.

이제 우리는 Cost = H(x) - y에 데이터를 대입하여 Cost의 총합을 구하는 것이 가능하고, Cost의 총합이 작은 Hypothesis일수록 데이터를 잘 대변하는 훌륭한 Linear Regression이라는 것을 알 수 있습니다.

 

하지만 아래 (1)의 Cost 그래프에서처럼 Cost는 양수일 수도, 음수일 수도 있습니다. 따라서 그래프(2)에서처럼 특정 그래프의 경우에는 Hypothesis와 실제 데이터 값의 차이가 크지만 총합은 0이 되는 문제가 생길 수 있습니다.

이러한 문제를 방지하고자 우리는 앞으로 총합을 구할 때 Cost값을 제곱하여 평균을 내는 방식(평균 제곱 오차, MSE)을 사용하며 최종 목적인 Cost function(비용 함수)은 다음의 수식으로 정의할 수 있습니다. 앞으로 우리의 목적은 이 비용 함수를 최소화하는 것입니다.

 

Cost function(비용 함수)

그래프 2.1 Cost (H(x) - y)를 표현한 그래프

 

 

그래프 2.2. Hyphotesis와 실제 데이터 값의 차이가 크지만. 비용의 총합은 0이 됩니다.

 

 

이번 글에서는 Regression과 Linear Regression의 정의와 기본적인 의미에 대해 살펴보았으며, Hypothesis와 Cost function을 정의하는 방법을 배웠습니다. 머신러닝, 딥러닝에서 learning의 목적은 Cost를 정의하고 이를 최소화하는 것입니다.